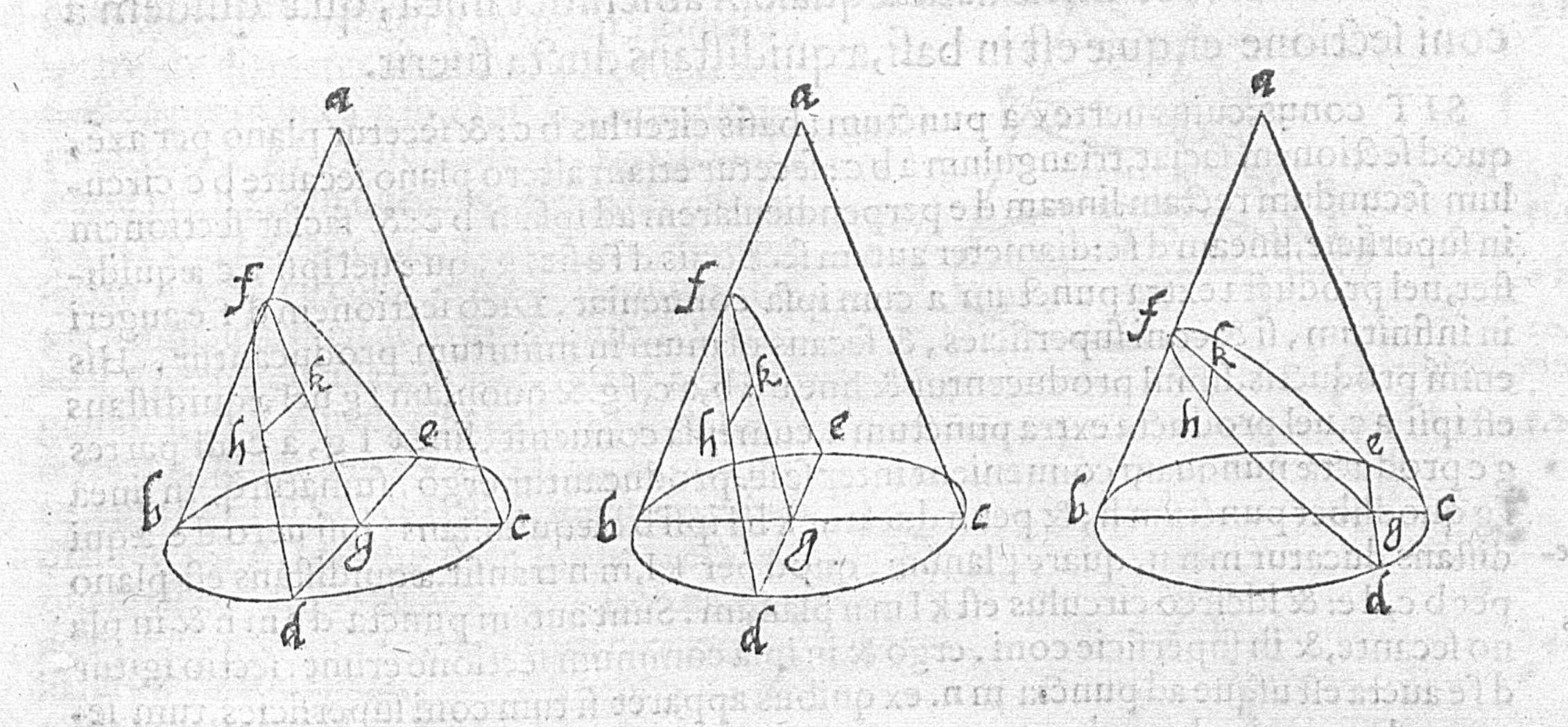
The figure here shows the basic types of conics and the angles at which they intersect a plane. A conic section (or conic) is a curve obtained as the intersection of a cone with a plane. Depending on the angle at which the plane intersects the curve three types of conic section can be obtained: hyperbola, parabola, ellipse. Euclid and Archimedes wrote lost treatises on conics; the first comprehensive text to reach us has been written by Apollonius (ca 220 - ca 170 BCE) from Pergamon, one of the main centers of Hellenistic learning (from which the term pergamena “parchment” derives). While, in part, “Elementary,” Apollonius’ Conics is not organized according to an axiomatic sequence in the manner of Euclid’s Elements; instead it forms a diverse collection of nearly independent treatises organized into eight books.
The first four books are preserved in the original Greek and have been first translated into Latin by Joannes Baptista Memus and published in Venice in 1537. Our edition is the much better translation by Commandino published in Bologna in 1566 together with other Greek mathematical texts. Books V-VII have been preserved into Arabics and have been translated into Latin first in 1175 in Toledo by Gerard of Cremona, the medieval translator of Ptolemy’s Almagest, then in 1710 by the famous astronomer Edmund Halley. The first published Latin translation has been made by Edmond Halley, most famous for having calculated the orbit of the eponymous comet.
Sources- Ludovico Geymonat (ed.) Storia del pensiero filosofico e scientifico. Milano, Garzanti, 1970-1972, vol. 1 p. 247.
- George Sarton, Introduction to the history of science, Baltimore: Williams & Wilkins Co., 1927-1948, vol. 1, pp. 173-175.
- Paul T Keyser and Georgia Irby-Massie (eds), The encyclopedia of ancient natural scientists : the Greek tradition and its many heirs, Milton Park, Abingdon, Oxon ; New York, NY : Routledge, 2008.
- Apollonius’s Conics The Greek and Arabic Traditions:
- http://individual.utoronto.ca/acephalous/Sidoli_On_Rashed_Decorps-Foulquier_Federspiel_2011.pdf
- Wikipedia Conics, Apollonios